Double Bounding Boxes
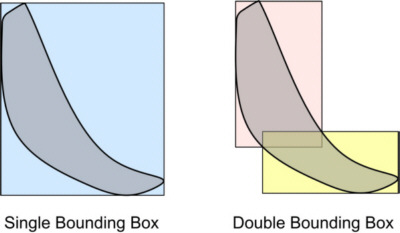
Minimal bounding rectangles are a simple and efficient tool for approximating geometries, particularly for accelerating spatial queries. If a spatial object fills a rectangular shape to a certain extent, then the minimal bounding rectangle is a reasonable approximation. Unfortunately some geo objects, such as streets or rivers, have a small area but large bounding rectangles. In our approach we suggest an approximation with two bounding rectangles instead of a single one. Since the corresponding shape provides a better approximation, we get a greater average benefit. We developed an efficient algorithm that computes the two rectangles with the theoretically smallest combined area that encloses a given geometry in O(n·log n) steps. The algorithm is presented in Jörg Roth:A runtime of O(n·log n) steps for n geometry points may be a crucial point for geometries with large amounts of geometry points. In a second approach, we introduce an approximation that requires O(n) steps but only produces approx. 11% more false hits compared to the theoretical optimum. The approximation is presented in Jörg Roth:You can find the slides of the talk in Rome here. |
 email
email